
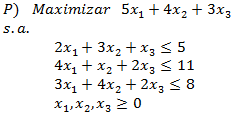
In two-dimensional cases, the value attained by the original variables as inferred from the table is indicated by a red dot in the corresponding graphic.įor details of the algorithm used, please refer to Chapter 3 of.
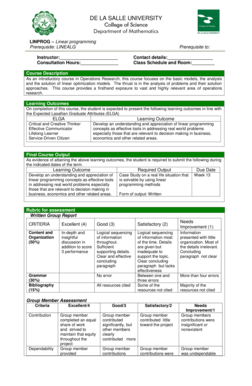
The value attained by the objective function at the end of phase 2 is highlighted in light blue. The pivot element is highlighted in light red. In this Demonstration, in the tables the values attained by the original variables that happen to be basic variables are highlighted in light green. If the value in the right-hand side (r.h.s.) column of the top row is negative at the end of phase 1, it means that the constraints are infeasible.Īn equality constraint is replaced by the corresponding greater-than-equal-to constraint and the lesser-than-equal-to constraint. If the linear programming problem immediately offers a basic feasible solution, phase 1 is bypassed. The second row from the top represents our actual objective function in phase 1.Īt the beginning of phase 2, the top row is dropped and the new top row represents the actual objective function.
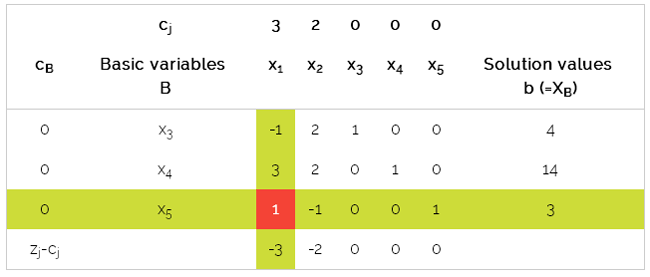
In phase 1, the top row of the table represents the objective equation that we try to minimize to zero in our search for a basic feasible solution. If the constraints are feasible, then the basic feasible solution obtained at the end of phase 1 is used in phase 2 to begin a search for the optimal solution (which lies at one of the corners of the convex polytope defined by the constraint equations). Artificial variables are introduced in phase 1 and dropped at the beginning of phase 2. Phase 1 of the two-phase simplex algorithm tries to find a basic feasible solution.


 0 kommentar(er)
0 kommentar(er)
